线性判别分析的原理与实践

介绍

线性判别分析（Linear Discriminant Analysis, LDA）是一种有监督式的数据降维方法，是在机器学习和数据挖掘中一种广泛使用的经典算法。
LDA的希望将带上标签的数据（点），通过投影的方法，投影到维度更低的空间中，使得投影后的点，按类别区分成一簇一簇的情况，并且相同类别的点，将会在投影后的空间中更接近。

LDA

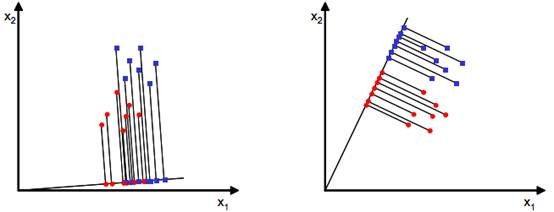
如上图所示（数据只有二维的情况），LDA希望能寻找到第二条直线，并将高维的数据投影到低维空间中，使得类之间耦合度低，类内的聚合度高。这样的话，接下来就可以方便利用低维的数据对数据进行分类。

理论基础

我们可以通过数学推导来获取这个最优的投影方向。假设我们共有${D_1,D_2,…,D_C}$类带有标签的数据，每个数据的特征维数为n维。首先求每个类别的中心（向量）为
$$ \mu_i = \frac{1}{n_i} \sum_{x \in D_i} x $$
其中$n_i$是类别i的数据总量。
假设我们想将数据投影到k维的空间中，我们需要一个$n \times k$大小的投影矩阵$W = [w_1,w_2,…,w_k]$，从而使得$y = W^T \cdot x$ 是一个k维的向量。也就是说把原始数据降低到了k维。

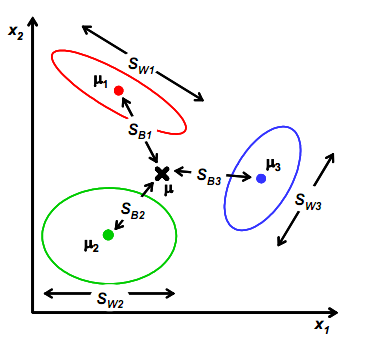
multi-dimension LDA

为了衡量经过投影矩阵W之后数据的离散情况，我们定义类内散列矩阵（Within-class scatter matrix）$S_W$和类间散列矩阵（Between-class scatter matrix）$S_B$。具体的推到过程如下:
首先我们可以得到投影后每个类别的中心为
$$\widetilde {\mu_i}=W^T \cdot \mu_i$$
因此，经过投影后每个类别点之间的方差为
$$ \widetilde{s_i} = \sum_{x \in D_i} (W^T \cdot x -\widetilde{\mu_i})^2 $$
注意到$\widetilde {\mu_i}=W^T \cdot \mu_i$，所以上式也可以写成
$$
\widetilde{s_i} = \sum_{x \in D_i} (W^T \cdot x -\widetilde{\mu_i})^2 =
\sum_{x \in D_i} (W^T \cdot (x - \mu_i))^2 =
\sum_{x \in D_i} W^T \cdot (x - \mu_i) \cdot (x - \mu_i)^T \cdot W
$$
将$\sum_{x \in D_i} (x - \mu_i) \cdot (x - \mu_i)^T $ 定义为类别i的类内散列矩阵$S_{W_i}$；因此所有类别内方差之和既为
$$
\widetilde{S} = \sum_{\forall i} \widetilde{s_i} = W^T \cdot (\sum_{\forall i} S_{W_i}) \cdot W
$$
其中$S_W = \sum_{\forall i} S_{W_i}$即为我们要求的类内散列矩阵。$\widetilde{S}$衡量了经过投影后每个类别间的接近程度，我们的优化目标是让该值尽可能的小。

接下来，我们来量化类别间的数据的离散程度。为了达到这个目的，首先我们求得所有类别的投影后中心，即每个类别的中心$\widetilde{\mu_i}$的中心
$$\widetilde{\mu} = \frac{1}{C} \sum_i {\widetilde{\mu_i}}$$
LDA 将类别间的离散程度定义为各类别中心$\widetilde{\mu_i}$到中心$\widetilde{\mu}$的距离平方和。由于每个类别中的样本数量可能不同，因此在计算的时候应该乘以一个权重$n_i / N$, 其中$N$是数据的总量。不过LDA的倍数不是很敏感，因此可以直接乘以一个系数$n_i$即可。也就是说，类别间的距离可以用如下公式衡量。
$$
\widetilde{T} = \sum_{i} n_i \cdot (\widetilde{\mu_i} -\widetilde{\mu})^2
$$
同理，注意到$\widetilde{\mu_i} -\widetilde{\mu} = W^T(\mu_i-\mu)$，其中$\mu$是未经投影的所有类别中心，计算方法相同。因此，以上表达式可以重新写成
$$
\widetilde{T} = \sum_{i} n_i \cdot (\widetilde{\mu_i} -\widetilde{\mu})^2
= \sum_{i} n_i \cdot W^T \cdot (\mu_i -\mu) \cdot (\mu_i -\mu)^T \cdot W
$$
其中 $S_B = \sum_{i} n_i \cdot (\mu_i -\mu) \cdot (\mu_i -\mu)^T$ 即为类间散列矩阵。$\widetilde{T}$衡量了经过投影后每个类别间的离散程度，我们的优化目标是让该值尽可能的大。

上述问题变成了一个多目标优化的问题，也就是说我们希望$\widetilde{S}$尽可能的小而$\widetilde{T}$尽可能的大。因此，我们可以将该多目标优化问题转化成求$\widetilde{T}/\widetilde{S}$的最大化问题。因此，该最大化目标函数可以写为
$$
J(W) = \frac{\widetilde{T}}{\widetilde{S}} = \frac{W^T \cdot S_B \cdot W}{W^T \cdot S_W \cdot W}
$$
接下来，我们添加一个约束条件$ ||W^T \cdot S_W \cdot W|| =1$ （不影响最终的结果，因为对于最优矩阵W，任意矩阵CW也是最优的，也就是说解有无穷多个，这样的限制条件相当于限制了C，因此可以求到唯一解）, 并采用拉格朗日乘子法求取函数在约束条件下的极值。具体过程如下：
$$L(W)=W^T S_B W - \lambda(W^T S_W W - 1) $$
对上式子进行求导，得到（该过程存在疑问）
$$\frac{dL}{dW}= 2S_BW-2\lambda S_W W=0 $$
$$\therefore S_BW = \lambda S_W W $$
$$\therefore {S_W}^{-1}S_BW = \lambda W $$
因此我们可以得到$ {S_W}^{-1}S_B w_i = \lambda_i w_i $（存在疑问）。也就是说，求最佳投影矩阵的问题变成了求矩阵${S_W}^{-1}S_B$的特征值和特征向量问题。最佳投影矩阵W的每一个列向量就是矩阵${S_W}^{-1}S_B$的一个特征向量。最后选取K个最大的特征值对应的特征向量作为矩阵W的每一列即可得到投影矩阵W。

在上述推导过程中，我们要注意几个问题。

由于矩阵${S_W}^{-1}S_B$不一定是一个对称的矩阵，因此LDA求得的特征值可能不是正交的，这一点和主成分分析（PCA）不同。
由于$\mu_i - \mu$的秩为1（因为是一个向量），因此$S_B$的秩至多为类别总数C（矩阵的秩小于等于各个相加矩阵的秩的和）。又因为知道$\mu$和其他C-1个$\mu_i$后，最后一个$\mu_i$可以直接计算出来，因此$S_B$的秩至多为C-1，也就是说降维的最大维度不会超过C-1。值得注意的是这个和数据的特征维度$n$没有关系，因此这也会导致LDA的一些不足。
为什么最后要选取特征值最大的K个特征向量来构成投影矩阵W呢？事实上，由于$ {S_W}^{-1}S_BW = \lambda W $，对于$J(W)$我们可以做如下的化简：
$$
J(W) = \frac{W^T \cdot S_B \cdot W}{W^T \cdot S_W \cdot W}
= \frac{W^T {S_W}^{-1} S_B W}{W^T \cdot W}
= \lambda
$$
从这个推导里面我们可以看出$\lambda$越大越好，因为我们的优化目标是让$J(W)$尽可能的大。

LDA的局限性

LDA最多将数据降维至C-1维，也就是说如果有两类数据，最终降维只能到1维，也就是说投影到一个直线上。这在很多情况下无法对数据进行很好的投影，例如下图中的几种情况。也就是说，LDA不适合对非高斯分布的样本进行降维。

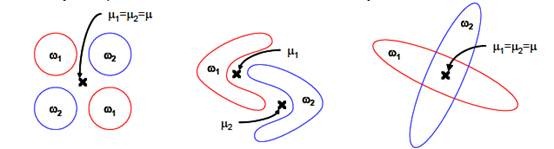
LDA limitation

LDA在样本分类信息依赖方差而不是均值时，效果不好，如下图所示。

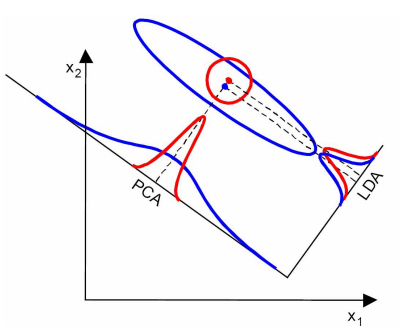
LDA limitation 2

LDA可能过度拟合数据。

一个简单的例子

假设我现在有两类数据，如下图所示。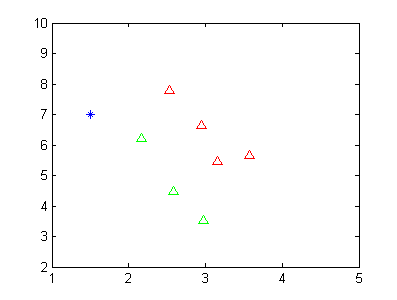
original data

其中红色的三角形代表一类数据，绿色的三角形代表第二类数据。蓝色的点代表未知样本点，我想通过LDA的方式判断其类别。当然从这个二维图中，我们可以看到该蓝色的数据点应该是属于第二类的（绿色）。

接下来，正文利用上面的LDA方法，首先求取每个样本的均值，得到$\mu_1 = [3.0525,6.3850]^T$ 以及 $\mu_2 = [2.57,4.733]^T$。接下来，利用公式求
$$
S_W = \sum_{i=1}^2 {\sum_{x \in D_i} (x-\mu_i)^T (x-\mu_i)}
$$
值得一提的是，在二维的特殊情况里面，不需要添加权重参数（这个可以在参考文献一里面得到解释）。再次之后，我们求取矩阵
$$
S_B = (\mu_1 - \mu_2)^T (\mu_1 - \mu_2)
$$
这里和上述推导不一致的原因是因为在二维的情况下，类间的离散程度之间使用$(\widetilde{\mu_1}-\widetilde{\mu_2})^2$来表示了。
得到$S_B$以及$S_W$之后，求取矩阵${S_W}^{-1}S_B$的特征值得到唯一的特征值8.3846以及对应的特征向量$v= [-0.9423,-0.3347]$。将两类数据按列排布，得到矩阵$D_1,D_2$，并分别求$v \cdot D_i$，得到两类数据的一维表示，如下图所示。

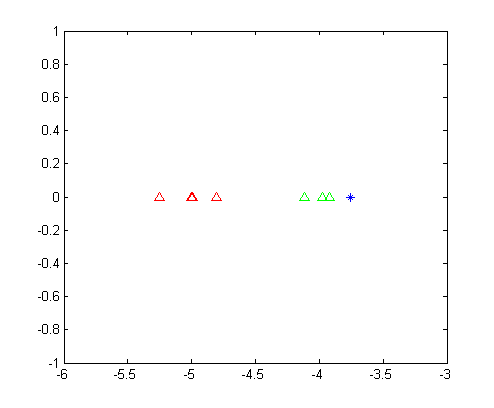
projection data

同理，我们可以将未知点和向量$v$做内积，并将结果绘制在图中。从这幅图里面我们可以清晰的看出，第一类数据和第二类数据被完美的分开了，并且可以明显的看出来，位置数据应该是属于第二类的。

源代码

data=[1	2.95	6.63
1	2.53	7.79
1	3.57	5.65
1	3.16	5.47
2	2.58	4.46
2	2.16	6.22
2	2.97	3.52];

type_one = data(1:4,2:3);
type_two = data(5:7,2:3);
plot(type_one(:,1),type_one(:,2),'r^');
axis([1,5,2,10])
hold on;
plot(type_two(:,1),type_two(:,2),'g+');
plot(1.5,7,'b*')


mean_one = mean(type_one);
mean_two = mean(type_two);
mean_all = mean(data(:,2:3));
s1=zeros(2,2);s2=s1;
for i=1:4
    s1=s1+(type_one(i,:)-mean_one)' *(type_one(i,:)-mean_one);
end

for i=1:3
    s2=s2+(type_two(i,:)-mean_two)' *(type_two(i,:)-mean_two);
end
sw=s1+s2;
sb=(mean_one-mean_two)'*(mean_one-mean_two);
mat=inv(sw)*sb;
[V,D]=eig(mat);
fv=V(:,2);

eigone=fv'*type_one';
eigtwo=fv'*type_two';

example=[1.5,7];
type = fv'*example';

figure;
plot(eigone,[0 ,0,0,0],'r^')
hold on;
axis([-6 -3, -1 1])
plot(eigtwo,[0 ,0,0],'g^')
plot(type,0,'b*')

参考文献

http://blog.csdn.net/ffeng271/article/details/7353834
http://www.cnblogs.com/LeftNotEasy/archive/2011/01/08/lda-and-pca-machine-learning.html

介绍
理论基础
LDA的局限性
一个简单的例子
源代码
参考文献