字符串匹配是一个很经典的问题。问题输入包括两个字符串：主串S和模式串P，而我们的任务是判断S中是否包含P。如果包含则返回S中出现的第一个P的位置（或S中出现的所有的P的位置），否则返回-1(NULL)。

在本文中，我主要讨论和讲解KMP字符串匹配算法的具体细节和背后的算法思想。在下文中，为了便于分析，我们记主串S的长度为n，模式串P的长度为m。此外，我们用符号i和j分别表示S和P正在匹配的字符所处的位置。

简单算法

一个最简单的算法（在下文中称为“简单算法”）是这样做的：

对于主串S中的每一个位置i，从该位置和模式串P从头开始匹配，每次最多需要进行m次比较操作。
如果一直比较到P的末尾字符还没有出现mismatch，那么说明S在位置i开始包含了一个模式串P。
如果没有比较到P的末尾字符便出现mismatch，则从主串S的i+1位重新和模式串P从头开始匹配。

由于S中一共有n个位置，所以这种算法的时间复杂度为O(n*m)。具体来讲，假设主串S是abacaabacabac，模式串P是abacab，那么简单算法的第一步是从S的0位（在本文的分析中，为了和程序对应，下标全从0开始）和P开始匹配。在这种情况下，如图1-(1)所示，当S和P比较到第5个元素时，发生mismatch。也就是说，当i=5, j=5时，S和P发生mismatch。简单算法的处理方式是：从主串S的位置1开始重新和模式串P从头进行匹配。也就是说，下一次比较的元素在S和P中的位置分别为i=i-(j-1), j=0（参考图1-(2)）。
next step of traditional alg when mismatch

可以看出，简单算法在发生mismatch时，i和j都要回退。在匹配过程中，回退的次数越多，距离越大，算法耗时越长。最坏的情况下，如果每次都在模式串的最后一位出现mismatch，那么总共需要的比较次数就是$n \times m$。

KMP算法

简单算法在出现mismatch时，主串比较的位置i会回退，导致一些没有意义的比较，那么我们如何优化算法减少无意义的比较呢？我们需要注意一个事实：当比较的位置从i退回到i-(j-1)后，在之后的比较中，一定存在某次比较，比较的位置回到i（不考虑在位置0直接mismatch的情况）。也就是说，i发生回退后一定会重新回到原位置。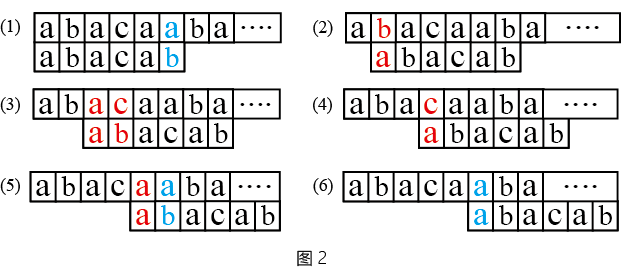
mismatch analysis
举个例子，如图2所示，在(1)中i=5,j=5时出现了mismatch。接下来，简单算法回退i和j，变成(2)所示的情况继续比较。当比较到(5)所示的情形时，i再次回到5，此时j的值是1。

既然i发生回退后一定会重新回到原位置，那么能否在发生mismatch时不回退i，直接让S[i]和模式串中的某个字符继续进行比较？这样子可以减少很多无意义的比较（图2中所有红色的部分）。答案是可以的，这就是KMP算法的核心思想。具体来说，对于KMP算法，如果S和P在i和j发生mismatch，则下一次比较时，i不变，j回退为某个值x（x < j）。

现在的问题在于我们如何求x的值。继续观察图2 (1)-(5)，我们可以发现，在(1)中出现mismatch后，算法执行到情况(5)时，i的值第一次重新回到5，此时j为1，就是我们要求的x。在字符串匹配中，有一个重要的性质我们需要注意：
当S和P的第i，j在进行比较时，那么S位于位置i-j到i-1的片段一定和P位于0到j-1的片段完全相同，即S[i-j:i]=P[0:j]（这里的表达方式和python中的切片完全相同）。举个例子来说，在(1)中，i=5,j=5时，所以S[0:5]=P[0:5]成立。

有了这个性质，当S和P在位置i，j发生mismatch时，应该有S[i-j:i]=P[0:j]。此外，当i回到之前mismatch的位置时，假设此时和其匹配的元素在P中的位置为x，则有S[i-x:i]=P[0:x]。注意到j > x，那么S[i-j:i]=P[0:j]同时也代表S[i-x:i]=P[j-x:j]。综合以上两个等式，我们可以得到
$$P[0:x]=P[j-x:j] \quad (1)$$
从图2中，我们也可以清晰的发现，在(5)中i=5，j=1正在进行匹配，这意味着S[4:5]=P[0:1]，即S[4]=P[0]。但是我们同时需要注意，在(1)出现mismatch时，S[4]是和P[4]相等的，因此我们可以得到P[0]=P[4]。

公式(1)描述了x必须满足的一个条件，但是凭此还不能确定x的值，这是因为对公式(1)来说，它的解可能不是唯一的。事实上，无论j取何值，x=0对公式(1)是恒成立的，这是因为P[0:0]=P[j:j]=空字符串。对于本例来说，当j=5时，x=1也可以使上式成立。那为什么x的值应该是1而不是0呢？这是因为我们需要找的是i的值第一次回到原位置时，相应模式串的匹配位置。我们知道在简单算法中，发生mismatch时，模式串整体后移一个单位并从头开始重新匹配，如果i的值会多次回到原始值，假设每次i回到原始值时，对应子串的位置分别为$x_1,x_2,…,x_n$，那么$x=x_1$一定是这里面的最大值，也就是说

$$x = \max \{ t | p[0:t]=p[j-t:j] \} \quad (2)$$

事实上，上述公式就是在求取，对模式串的子串P[0:j]，能使前t个元素和后t个元素相等的t的最大值。例如对模式串abacab，但是在j=5时mismatch，子串P[0:5]为abaca，只有前1个元素和最后一个元素相等，因此x=1。

从公式(2)我们可以看出，x的值只和j以及模式串P有关。因此我们可以在匹配算法开始前计算出每一个j所对应的x，形成一个数组，一般称之为next数组。nxt[j]表示当在P的第j个字母出现mismatch时，下一次P中参与匹配的字母位置（主串匹配的位置不变）。

需要注意的是，我们刚才所有的讨论都是当mismatch时j不为0的情况。事实上，如果mismatch时j=0，那么按照传统算法，下一次匹配时的位置为i=i+1，j=0。也就是说，i是增加的，反而不会回退。由于KMP的基本思想是mismatch是不改变i的值，那么在这种情况下，我们需要做特殊处理，令下次匹配的位置为i=i，j=-1，这就符合KMP的基本思想了。说了这么多，我只是想强调nxt[0]一定为-1，并且需要在KMP算法中做特殊处理。

说到这儿了，我们就可以开始写代码了，python实现的参考代码如下。这里我只展示在已经获得next数组的情况下，如何找到第一个出现的字串位置。

def kmp(S,P):
    i = 0 ; j = 0
    nxt = get_next(P) #计算next数组，之后讨论
    while i < len(S):
        if j == -1 or S[i] == P[j]:
            # 匹配成功则继续匹配S和P的下一位
            # 注意j=-1时，意味着我们应该直接比较S和P的下一位
            i += 1 ; j += 1
        else:
            # 匹配失败时，i不动，j回退到之前计算的nxt[j]
            j = nxt[j]

        # j==len(P)，说明已经匹配了一个完整的模式串
        if j == len(P):
            return i-j
    # 不存在该模式串
    return -1

如果是需要求出所有的模式串出现的位置，改成如下代码即可

def kmp_all(S,P):
    i = 0 ; j = 0
    nxt = get_next(P)
    found_pos = []
    while i < len(S):
        if j == -1 or S[i] == P[j]:
            i += 1 ; j += 1
        else:
            j = nxt[j]

        # 注意下面部分的变化
        if j == len(P):
            found_pos.append( i-j )
            j = nxt[j]
    return found_pos

需要注意的是，nxt数组的长度是要比模式串的长度多1的，nxt的最后一个元素代表了出现一次完整匹配的话，如果还想继续匹配，当前位置i应该和模式串中哪个位置进行匹配。对于只找一个模式串的情况，可以不进行计算。

对于KMP算法来说，在其在图2(1)，i=5,j=5发生mismatch后，它的一下次匹配的位置便是图2(5)，i=5,j=1，省略了图2中所有的红色比较操作，大大加快了算法的速度。有些读者可能会担心省略了这些比较，算法会不会出错，丢失一些匹配的位置？

假设主串S和模式串P在图3(1)中位置i，j发生mismatch，根据KMP算法，下次S和P匹配的位置即为图2(2)中i,x。相比于简单算法，图2中虚线框内所有的情况全部跳过，那么这样直接跳过是安全的么？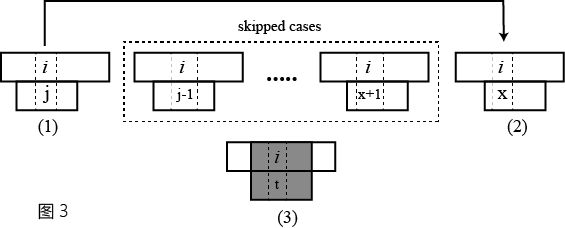
correctness analysis
我们假设这样做不安全，也就是说在skipped cases中存在一种情况，如图3(3)所示，S的一部分和P完全相同，即存在一个完整匹配。那么在这种情况下，按照简单算法的思路，S和P的位置i和t（t介于j-1和x+1之间）的元素一定会进行比较。因此，主串S的匹配位置第一次重回i时所对应的元素在P中位置应该大于或等于t，而不是x。但这和我们的假设矛盾，因此skipped cases中不可能存在图3(3)所示的情况。

上述性质之所以成立，其主要原因是，我们规定x是主串S的匹配位置第一次重回i时所对应的元素在P中位置，如果不是第一次，算法的正确性是无法保证的。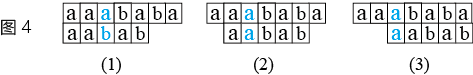
no name
如图4所示，当S和P在(1)发生mismatch后，i第一次回到位置2的情况如(2)所示，第二次回到位置2的情况如(3)所示。可以看出，如果在(1)发生mismatch后，不回退i的位置，直接让i和j=0进行匹配（(3)所示的情况），那么(2)这个完整匹配将被跳过，算法错误。

next数组的计算

接下来我们讨论如何计算next数组。最简单的情况下，我们可以一步步循环，并利用公式算出next，不过这样的效率并不是很高。

事实上，我们可以通过将模式串和自身进行匹配计算next的值。具体来说，如果模式串i和j的位置要进行匹配，那说明模式串$S[i-j:i] = S[0:j]$，这也就意味著如果在i的位置发生mismatch，那么对于$S[0:i]$ 来讲，它前j个字符和后j个字符是一样的。所以在i发生mismatch，我们只要匹配模式串的第j+1个位置即可，而他的下标刚好是j。

def get_next(p):
    # next数组的前两位一定是-1和0
    nxt = [-1,0]
    i = 1 ; j = 0 # 初始化很重要
    # 模拟匹配过程求取next
    while i < len(p):
        if j == -1 or p[i] == p[j]:
            i += 1 ; j += 1
            nxt.append(j) # nxt[i]=j
        # 注意else分支进入的次数一定比if少
        else:
            j = nxt[j]
    return nxt

算法时间复杂度

KMP算法由两部分组成，即主程序和get_next。这两部分构造是相似的，我们先分析get_next的时间复杂度。具体来讲，我们可以发现在整个while循环中，if分支最多进入len(p)次，也就是m次，问题是else分支进了多少次。

事实上，我们也不清楚else分支进入了多少次，但是我们可以肯定进入else的次数一定小于等于进入if 的次数。这是因为进入else分支时，j的值会减少，至少减少1，最低值为-1；由于j的值只有在if分支才会增加，因为减少的总值不可能大于增加的总值，所以便有了以上的结论。因此我们可以断定get_next的时间复杂度为O(m)。

同理，我们也可以算出KMP主程序的时间复杂度为O(n)（不包括get_next的情况下），因此算法总得时间复杂度就是O(n+m)。

参考文献

简单算法
KMP算法
1. next数组的计算
2. 算法时间复杂度
参考文献