主成分分析的原理与实践

介绍

主成分分析（Principal Components Analysis， PCA）和之前说到的线性判别分析一样，都是一种广泛使用的数据将维方法。PCA是一个和LDA非常相关的算法，从推导、求解、到算法最终的结果，都有着相当的相似，不过它和LDA也有一些不同的地方。

首先，PCA是一种无监督的数据降维方法。也就是说，他的输入数据没有标签来指示它是哪一个类别的。其次，它的降维目标和LDA不同。它的目标是通过某种线性投影，将高维的数据映射到低维的空间中表示，并期望在所投影的维度上数据的方差最大（损失的信息最少），以此使用较少的数据维度，同时保留住较多的原数据点的特性，投影时没有利用任何数据内部的分类信息。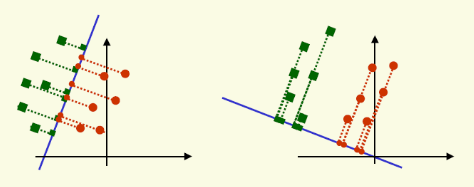
Illustration of PCA and LDA
如上图所示，图的左边是PCA，它所作的只是将整组数据整体映射到最方便表示这组数据的坐标轴上，映射时没有利用任何数据内部的分类信息。
图的右边是LDA，可以明显看出，两类输入映射到了另外一个坐标轴上，有了这样一个映射，两组数据之间的就变得更易区分了(在低维上就可以区分，减少了很大的运算量)。

PCA的理论基础

最大化方差理论

在信号处理中认为信号具有较大的方差，噪声有较小的方差，信噪比就是信号与噪声的方差比，越大越好。对于一组二维的数据来说，我们希望选择一个具有最大化方差的投影方向，这样子损失的信息（噪声）可以达到最小，也就是说方差最大和损失的信息最少这两个目标在PCA中是等价的。其实，通过两种不同的目标去做推导，得到的理论结果也是一样的（具体可见参考文献2）。

推导过程

在这边文章里面，我们采用最大化数据投影后的方差作为优化目标决定数据的投影方向。
假设现在的投影向量为$w$（假设投影到一维的情形），所有数据的集合用符号$D$表示，数据总量为$N$。首先我们获取原始数据的中心，
$$
u = \frac{1}{N} \sum_{x \in D} x
$$
那么经过投影后，数据中心为$u’ = w^Tu$. 那么投影后数据的方差可以表示为
$$
Var = \sum_{i=1}^N {(w^Tx_i - u’)^2} = \sum_{i=1}^N w^T(x_i - u)(x_i - u)^Tw
$$
令$ S= \sum_{i=1}^N (x_i - u)(x_i - u)^T$，则$ Var = \sum_{i=1}^N w^TSw $. 事实上，当数据只有两维的时候：
$$S = \begin{bmatrix}
{\sum (d_1 - \overline{d_1})^2}&{\sum (d_1 - \overline{d_1})(d_2 - \overline{d_2})}\
{\sum (d_1 - \overline{d_1})(d_2 - \overline{d_2})} & \sum (d_2 - \overline{d_2})^2
\end{bmatrix}$$
其中$d_i$表示 x 的第 i 个维度的数据，$\overline{d_i}$表示其均值。所以，不难发现：
$$S = N \times \begin{bmatrix}
cov(d_1,d_1)& cov(d_1,d_2)\
cov(d_2,d_1) & cov(d_2,d_2)
\end{bmatrix}$$
也就是说，事实上$S$是协方差矩阵的常数倍，又因为常数不影响投影方向的求解，所以我们可以在求解的时候使用数据的协方差矩阵即可。
回到推导中来，要想使$ Var = \sum_{i=1}^N w^TSw $达到最大，同样我们添加约束条件$||w^Tw||=1$并使用拉格朗日乘子法，得到
$$
L = w^TSw - \lambda(w^Tw)
$$
因此，通过求导得到
$$
\frac{dL}{dw} = 2Sw-\lambda 2w
$$
令上式等于0, 求取最大值，得到
$$
Sw = \lambda w
$$
于是该问题再次变成了一个求取矩阵S的特征向量问题。当降维数量大于1的时候，我们只需要选其矩阵S前K大特征值所对应的特征向量即可。

一个简单的例子

假如说我们现在有一组二维的数据，并且我们想通过PCA方法将数据降低到一维。原始数据的图像表示如下。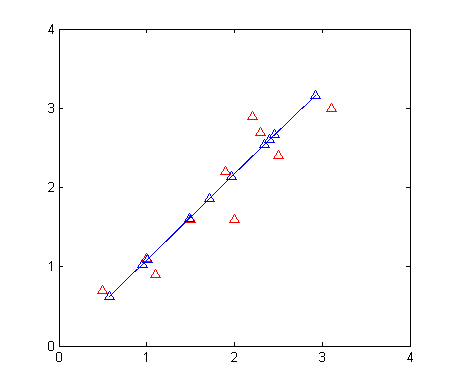
original data fig
按照上面的理论推导，为了得到最佳的投影方向，我们需要计算矩阵$S$。但是通过上述分析我们也可以直接使用数据的协方差矩阵。
$$
C = \begin{bmatrix}
cov(d_1,d_1)& cov(d_1,d_2)\
cov(d_2,d_1) & cov(d_2,d_2)
\end{bmatrix}
= \begin{bmatrix}
0.6166 & 0.6154\
0.6154 & 0.7165
\end{bmatrix}
$$
可以看到，该矩阵是一个对称的矩阵，元素$C_{1,2}$和$C_{2,1}$是相等的。接下来，我们计算协方差矩阵$C$的特征值和特征向量，得到两个特征值0.0491，1.2840和对应的特征向量，分别为
$$
v_1 = [-0.7352,0.6779], v_2 = [0.6779,0.7352]
$$
注意，由于协方差矩阵是对称的，这里得到的两个特征向量一定是正交的，这一点和LDA方法不太一样。在这两个特征向量里面选取特征值较大的对应的特征向量，即$w = [0.6779,0.7352]$
接下来，通过这个向量，我们可以将原始数据降维到一维空间中，即
$$
FinalData = oriData*w
$$
这样我们就将一组二维的数据投影到了一维的空间中，并且尽最大可能保留的数据的信息。
为了将投影后的数据可视化出来，我们可以通过投影向量$w$重建原始数据$oriData$，因为根据上式，我们可以得到
$$
oriData’ = FinalData \cdot w^{-1} = FinalData \cdot w^T
$$
值得注意的是，重建后的数据和原始数据是不完全一样的，因为我们在做投影的时候已经损失了一部分的信息。事实上，重建后的数据刚好就是原始数据在投影向量上的那些点构成的数据，具体可见下图。

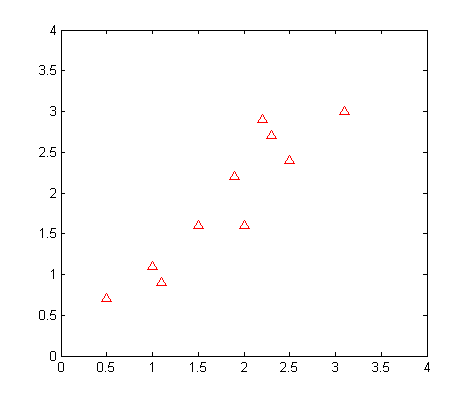
final result presenation

在这幅图中，蓝色的点表示重建后（投影数据的二维表示），可以看出PCA最大限度地保持了数据点之间的相对位置关系，降低了数据的维度，方便后期的处理。

总的来说, 假如说你的数据是$M \times N$维度的，也就是一共有N个数据，每个数据时M维度的，可以得到一个MxM的协方差矩阵，对协方差矩阵求其特征值以及特征向量。选取其中几个特征维度，一般是特征向量较大的几个特征维度，假如说这样得到了K个维度，则把这K个特征值对应的向量拿出来，得到一个KxM的特征矩阵。将这个矩阵和原始的数据矩阵相乘，即
$$ EigenMat_{k \times m} \times Data_{m \times n} = NewData_{k \times n} $$

这样得的到数据$new data$就降低成为K维的了。

代码实现

clc;clear;close all;
mdata=[2.5 2.4
0.5 0.7
2.2 2.9
1.9 2.2
3.1 3.0
2.3 2.7
2 1.6
1 1.1
1.5 1.6
1.1 0.9];

x=mdata(:,1);
y=mdata(:,2);
plot(x,y,'^r');
covmatrix=cov(x,y);
[V,D]=eig(covmatrix);
% the importance of PCA
fvector=V(:,2);
finaldata=mdata*fvector;
% reconstruct the data
lastdata=finaldata*fvector';
lx=lastdata(:,1);
ly=lastdata(:,2);
hold on;
axis([0,4,0,4])
plot(lx,ly,'b^-');

参考文献

http://www.cs.otago.ac.nz/cosc453/student_tutorials/principal_components.pdf
http://www.cnblogs.com/LeftNotEasy/archive/2011/01/08/lda-and-pca-machine-learning.html

介绍
PCA的理论基础
1. 最大化方差理论
2. 推导过程
一个简单的例子
代码实现
参考文献